Базові поняття статистики

Оксана Кудла, учитель математики
Єзупільського НВК Тисменицького району Івано-Франківської області

Цільова група:

• учні 9 класу

Тривалість:

• 90 хв. (2•45 хв.)

Мета:

• ознайомити учнів з основними поняттями математичної статистики;
• розвивати вміння подавати статистичні дані у вигляді таблиць, графіків та відшукувати центральні тенденції вибірки;
• формувати підприємницькі компетентності, використовуючи методи розв’язування статистичних задач.

Операційні цілі (завдання):

Після закінчення уроку учень

знає

• визначення статистичного ряду, вибірки, моди, медіани;

розуміє

• значення статистики для ведення успішної підприємницької діяльності;

вміє

• створювати статичні таблиці на основі вибірки;
• знаходити частоту, відносну частоту та середнє значення вибірки;
• будувати полігон частот та гістограму;

може

• аналізувати проблемну ситуацію;
• прогнозувати майбутні результати;
• оцінювати та усувати ризики;
• шукати оптимальні шляхи вирішення проблеми;
• брати на себе відповідальність;
• спілкуватися, висловлювати свою думку та захищати її;
• співпрацювати в команді.

Методи і техніки:

• мозковий штурм»;
• Пазли» / «Ажурна пилка»;
• робота в групах.

Обладнання:

• маркери, ручки, олівці;
• аркуші А4, А3;
• аркуші в клітинку;
• лінійки, ножиці, клей.

Допоміжні матеріали:

Додаток 1. Картка соціологічного опитування.

Додаток 2. Опорний конспект «Основні поняття статистики».

Додаток 3. Картки для вправи «Ажурна пилка».

Додаток 4. Практичне завдання.

Додаток 5. Картка самооцінювання учня з теми «Статистика».

Додаток 6. Діагностична картка «Оцінювання роботи малої групи».

Хід уроку

1. Вступна частина

1.1 Нагадайте учням, що основна мета вивчення теми «Елементи прикладної математики» - це оволодіння найпростішими способами подання, обробки й оцінювання інформації про реальні фізичні, соціальні, хімічні та інші процеси.

1.2 Змоделюйте для учнів ситуацію у вигляді проблемної задачі: Власник крамниці дізнався про розпорядження міністерства освіти щодо участі учнів 9-х класів у юнацькій спортивній олімпіаді. Він має можливість закупити велику партію спортивного взуття і мусить знати, яку кількість кросівок різного розміру для цієї вікової категорії необхідно закупити.

1.3 Запропонуйте учням згенерувати пропозиції - як у найкоротший термін власник магазину має отримати таку інформацію, якщо кількість учнів 9-х класів в області перевищує 100000? Нагадайте, що неправильних відповідей не буває. Запишіть пропозиції учнів на дошці. Будьте готові отримати такі варіанти: опитати в Faсebook, Twitter, інших соціальних мережах, розіслати листи електронною та звичайною поштою, дізнатись у школах домашні адреси учнів і пройтися по домівках тощо.

Коротко обговоріть кожний спосіб з погляду поданих нижче критеріїв:

• скільки учнів можна опитати за допомогою кожного з запропонованих методів?
• чи реально дізнатися розмір взуття всіх учнів?
• скільки часу буде витрачено на кожен метод (здобування адрес, спілкування в соціальних мережах тощо)?
• скільки працівників треба задіяти, щоби якнайшвидше здобути максимальну кількість інформації?
• скільки коштів треба витратити, щоб добратися в різні населені пункти області?

Наостанок запитайте учнів про те, що вони думають про необхідність опитувати всіх дев’ятикласників області? Вислухайте їхні думки і залишіть питання відкритим.

1.4 Запропонуйте 2 учням представити на дошці результати опитування, проведеного у паралельних класах щодо розміру взуття хлопчиків (Додаток 1).

Запропонуйте всім визначити з таблиць:

• Чи є однакові розміри взуття в обох досліджуваних групах?
• Чи є розміри, на які натрапляємо найчастіше чи найрідше в кожній групі? Які?
• Чим подібні й чим вирізняються обидві групи даних?
• Чи можна знехтувати найменшим і найбільшим значеннями з погляду продавця крамниці? Чому?
• Чи достатньо цієї інформації, щоб приблизно передбачити потребу в цих розмірах взуття у всіх навчальних закладах?
• Чи зручно опрацьовувати цей числовий ряд у такому невпорядкованому вигляді?

Повідомте учням, що з великих обсягів даних, які необхідно опрацювати, створюють вибірку меншого обсягу й опрацьовують її з деякою долею похибки. Скажіть, що існують методи, за допомогою яких можна визначити кількість елементів вибірки, що буде найбільш правдоподібно відображати реальний стан речей, але ці методи не вивчають у шкільному курсі. І для такої вибірки даних існують більш зручні форми запису та способи опрацювання, ніж ті, що були представлені біля дошки.

1.5 Повідомте учням тему і мету уроку - ознайомитися з основними поняттями математичної статистики, навчитися подавати статистичні дані у вигляді таблиць і графіків, відшукувати центральні тенденції, здійснювати найпростіше прогнозування.

2. Основна частина

2.1. Запропонуйте учням самостійно ознайомитися з основними поняттями та визначеннями математичної статистики. Для цього роздайте їм опорні конспекти (Додаток 2). Запропонуйте прочитати матеріал, підкреслити нові терміни. Через 2-3 хвилини запитайте в учнів, які терміни чи визначення залишилися їм незрозумілі. Поясніть їх.

2.2. Запропонуйте учням на основі представлених даних проблемної задачі назвати обсяг вибірки, варіанти вибірки, визначити декілька частот.

2.3. Повідомте учнів, що далі вони будуть працювати методом, який називається «ажурна пилка». Цей метод допоможе їм самостійно ознайомитися з великим обсягом матеріалу, сприятиме вмінню слухати інших, обговорювати, ставити запитання. Наголосіть, що, згідно з правилами цього методу, кожен з учнів бере на себе відповідальність за здобуті на уроці знання і від його власної праці залежатиме якість завдання, яке виконала вся група.

2.4. Поділіть клас на 5 груп і скажіть, щоб кожна група зайняла місце за окремим столом. Для поділу на групи використайте картки 5 різних кольорів, на кожній з яких записані цифри від 1 до 5. Групи формуйте за отриманим номером. Поясніть учням правила цього методу (див. розділ «Інтерактивні методи навчання»). Роздайте групам підготовлені тексти (Додаток 3). Наголосіть, що після того, як усі члени групи прочитають тексти, вони мають обговорити цей матеріал і впевнитися, що всі члени експертних груп правильно його зрозуміли, уміють розв’язати запропоновані задачі. Найважливіше, на що важливо звернути увагу, - це виділити головне з тексту, щоб пояснити матеріал іншим учням. Відведіть на це приблизно 5 хвилин.

2.5. Перейдіть до другого етапу методу «ажурна пилка», запропонуйте учням пересісти за інші столи, об’єднавшись у групи за кольором отриманої картки. Наголосіть, що від того, як вони працюватимуть, буде залежати успіх усієї групи. Попередьте, що другий етап триватиме 10 хв. Пам’ятайте, що Ви повинні бути тільки пасивним спостерігачем - прислухайтеся, чи правильно подають матеріал експерти, намагайтеся не поправляти їх, а запропонуйте іншим учасникам ставити запитання до експертів. Втручайтеся тільки у разі суперечки або конфлікту.

2.6. Коли завершиться час, перепитайте учнів, чи впоралися вони з поставленим завданням і чи готові продовжувати. При потребі додайте час на закінчення. Запропонуйте групам залишатися на своїх місцях і роздайте завдання (Додаток 4). Наголосіть, що тепер вони зможуть застосувати здобуті знання на практиці. Також роздайте групам підготовлені великі аркуші паперу, фломастери, ножиці, клей, папір у клітинку та інше. Повідомте, що на виконання завдань групи мають 10 хвилин, а після закінчення роботи один учень від групи має представити результати.

2.7. Вислухайте представлення виконаної роботи від груп. Обговоріть результати, особливо якщо виявиться, що в різних груп вони відрізняються. Важливо вислухати кожну групу в тій частині завдання, де відбувався аналіз проблемної ситуації. При потребі заохочуйте інших учнів висловлювати власну думку щодо коректності зроблених висновків, правильності застосованих методів.

3. Підсумкова частина

3.1. Підведіть підсумки уроку. Запитайте учнів, де в житті вони бачать застосування цих методів, чим було корисне проведене опитування для кращого усвідомлення навчального матеріалу.

3.2. Запропонуйте учням провести самооцінювання набутих знань (Додаток 5) й оцінити співпрацю групи (Додаток 6).

3.3. На домашнє завдання запропонуйте учням підібрати власні приклади до вивчених методів і понять за статистичними даними, взятими з різних галузей та додаткової літератури (з історії, географії, економіки тощо), та розв’язати придумані вправи на обробку й аналіз статистичних даних.

3.4. Подякуйте учням за урок, називаючи конкретно їхні якості, за які ви вдячні (наприклад: за активність, уміння аналізувати, креативність тощо).

 

Додаток 1

Картка соціологічного опитування

Група ________________________                              Опитування проводив _____________________

Дата __________________

 

Додаток 2

Опорний конспект «Основні поняття статистики»

Статистика - це наука про одержання, обробку й аналіз кількісних даних, які характеризують масові явища.

Математична статистика - розділ математики, який присвячений методам збору й обробки математичних даних та їх використанню для наукових і практичних спостережень.

Будь-яке статистичне дослідження починається з цілеспрямованого збору інформації. Зібрані дані можуть бути представлені у вигляді набору чисел, записаних у порядку їхнього надходження. Їх важко осягнути і зробити якісь висновки. Тому первинні дані потребують обробки. Зібрану інформацію зручно подавати у вигляді таблиць, графіків, діаграм.

Схема статистичного спостереження:

Збирання даних → Оброблення даних та їхнє подання у зручній формі → Аналіз даних → Висновки й рекомендації.

Основні поняття математичної статистики

1. Статистичні дані - сукупність чисел, які дають кількісну характеристику ознак певних об’єктів та явищ, що нас цікавлять (наприклад, учні 9-х класів, населення регіону, зоряне небо, флора чітко окресленої території).

2. Відібрану для спостереження сукупність об’єктів називають вибірковою сукупністю, або вибіркою.

3. Кількість об’єктів сукупності називають об’ємом сукупності.

4. Кількість об’єктів вибірки називають об’ємом вибірки.

5. Статистичним рядом називають упорядковану за зростанням значень вибірку.

6. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; впорядковану за зростанням значень послідовність варіант називають варіаційним рядом.

7. Частоти - числа, які показують, скільки разів повторювалося кожне значення ознаки сукупності.

8. Відношення частоти до об’єму вибірки називають відносною частотою.

Приклад. Нехай дано вибірку:

2; 4; 5; 5; 6; 2; 3; 3; 4; 4; 4; 2; 3; 3; 3; 4; 4; 5; 5; 5;

Її статистичний ряд матиме вигляд:

2; 2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 6.

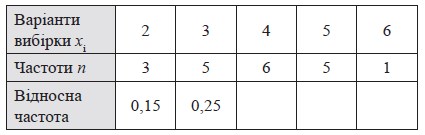
х1 = 2; х2 = 3; х3 = 4; х5 = 5; х6 = 6 - варіанти вибірки; 2; 3; 4; 5; 6 - варіаційний ряд. Частота варіанти х1 дорівнює 3; варіанти х2 - 5; варіанти х3 - 6; варіанти х4 - 5; варіанти х5 - 1. Відносна частота варіанти х1 дорівнює 3/20 = 15%; варіанти х2 - 5/20 = 25%. Відносну частоту можна подавати у відсотках або звичайних чи десяткових дробах.

Статистична таблиця розподілу вибірки:

 

Додаток 3

Картки для вправи «Ажурна пилка»
Обробка й аналіз статистичних даних

Група 1

Для наочного представлення статистичного розподілу користуються графічним зображенням варіаційних рядів - діаграмами, графіками, полігоном, гістограмами та ін. Діаграми та графіки вам відомі. Розгляньмо інші види графічного зображення.

Для побудови полігона на осі ОХ відкладають значення варіант хi, на осі ординат - значення частот п. Точки (хі, пі) з’єднують відрізками прямих і одержують полігон частот.

Приклад 1. Дано статистичний розподіл вибірки обсягом N = 20.

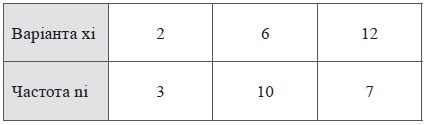
Побудуємо полігон частот цього статистичного розподілу:

Малюнок 1. Полігон частот

Приклад 2. Економіст, аналізуючи тарифні розряди працівників одного з цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди:
4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 - вибірка, що піддається обробці.

Статистичний ряд цієї вибірки:
2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6;

Статистична таблиця розподілу вибірки:

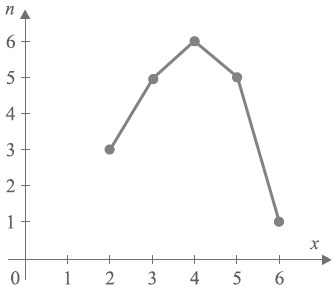
Малюнок 2. Полігон частот

Група 2

Для наочного представлення статистичного розподілу користуються графічним зображенням варіаційних рядів - діаграмами, графіками, полігоном, гістограмами та ін. Діаграми та графіки вам відомі. Розгляньмо інші види графічного зображення.

Гістограмою частот називають східчасту фігуру, яка складається з прямокутників, основами яких є інтервали значень ознаки, а висота пропорційна частоті інтервалу.

Приклад 1. Дев’ятикласники однієї школи написали контрольну роботу. З них 16 виконали завдання на високому рівні, 31 - на достатньому, 33 - на середньому, 7 - на початковому. Це кількісні характеристики проведеної контрольної роботи. Їх можна подати у вигляді таблиці:

Побудуємо гістограму за цими даними:

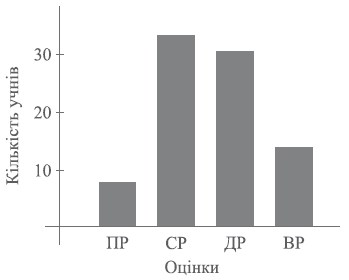
Малюнок 3. Гістограма

Приклад 2. Економіст, аналізуючи тарифні розряди працівників одного з цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди:
4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 - вибірка, що піддається обробці.

Статистичний ряд цієї вибірки:
2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6;

Статистична таблиця розподіл вибірки:

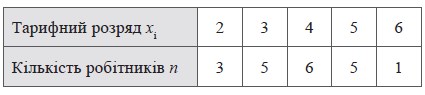
Малюнок 4. Гістограма

Група 3

Розгляньмо способи оцінки даних за розподілом частот. Їх метою є, як прийнято говорити в статистиці, виявлення міри центральної тенденції (центрального положення).

Мода вибірки - це значення ознаки, яка найчастіше повторюється у вибірці.

Приклад 1. Нехай дано вибірку:
2, 3, 4, 4, 6, 6, 6, 7, 7, 8.

Знайдемо центральні тенденції вибірки.

Розв’язок

Мода даної вибірки Мо = 6, бо число 6 трапляється найчастіше.

Вибірка може не мати моди, наприклад:
4, 5, 6, 7, 8;

мати дві моди:
2, 3, 4, 4, 5, 6, 6, 7, 8.

Приклад 2. Економіст, аналізуючи тарифні розряди працівників одного із цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди:
4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 - вибірка, що піддається обробці.

Розв’язок

Статистичний ряд цієї вибірки:
2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6.

Статистична таблиця розподілу вибірки:

Мода даної вибірки Мо = 4, бо число 4 трапляється найчастіше (6 разів). Тобто в одному з цехів заводу найбільше є робітників 4-го тарифного розряду.

Моду в статистиці застосовують тоді, коли слід охарактеризувати показник, який найчастіше трапляється в сукупності. Наприклад, під час вивчення цін на ринку встановлюємо ціни, які трапляються найчастіше; при встановленні найбільш ходового розміру взуття й одягу визначаємо той, який користується найбільшим попитом. Ці показники дають змогу спланувати, які товари необхідно виробляти в більшій кількості, а також які товари поставляти на ринок і за якими цінами.

Група 4

Розгляньмо способи оцінки даних за розподілом частот. Їх метою є, як прийнято говорити в статистиці, виявлення міри центральної тенденції (центрального положення).

Медіана вибірки - це число, яке «поділяє» навпіл упорядковану сукупність усіх значень вибірки, так що одна половина значень більша від медіани, а друга - менша.

Нехай дано вибірку: 1, 3, 2, 4, 5, 2, 3, 4, 1, 6, 4.

Упорядкуємо її: 1, 1, 2, 2, 3, 3, 4, 4, 4, 5, 6.

Медіана цієї вибірки дорівнює 3, бо число 3 «поділяє» впорядковану вибірку навпіл. Якщо впорядкована вибірка має парне число значень, то її медіана дорівнює півсумі двох її серединних значень. Наприклад, для вибірки 1, 2, 3, 3, 3, 4, 4, 5, 6, 6 медіана

Me = (3 + 4) / 2 = 3,5

Приклад 1. Нехай дано вибірку:
2, 2, 3, 4, 4, 6, 6, 6, 7, 7, 8.

Знайдемо центральні тенденції вибірки.

Розв’язок

Медіана даної вибірки Ме = 6, бо вибірка має непарне число значень і її медіана є середнім значенням.

Приклад 2. Економіст, аналізуючи тарифні розряди працівників одного з цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди:
4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 - вибірка, що піддається обробці.

Розв’язок

Статистичний ряд цієї вибірки:
2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6;

Статистична таблиця розподілу вибірки:

Медіана даної вибірки Ме = 4, бо вибірка має парне число значень і її медіана дорівнює півсумі двох її середніх значень (4 + 4) / 2 = 4 .

Сума відхилень варіант від медіани є найменшою величиною. Ця властивість медіани зумовлює її практичне використання, наприклад, у маркетингу, будівництві - під час планування шкільних та дошкільних закладів, кінотеатрів, торговельних закладів, зупинок міського транспорту тощо.

Група 5

Розгляньмо способи оцінки даних за розподілом частот. Їх метою є, як прийнято говорити в статистиці, виявлення міри центральної тенденції (центрального положення).

Середнім значенням вибірки називають середнє арифметичне всіх її значень.

Приклад 1. Нехай дано вибірку:
2, 3, 4, 4, 6, 6, 6, 7, 7, 8.

Знайдемо центральні тенденції вибірки.

Розв’язок

Середнє значення вибірки:
(2 + 3 + 4 + 4 + 6 + 6 + 6 + 7 + 7 + 8) / 10 = = 53 / 10 = 5,3

Приклад 2. Дано вибірку вимірювання повітря температури (t, °С) у першій декаді квітня: 5; 6; 4; 3; 4; 5; 6; 2; 4; 6. Складіть статистичний ряд; визначте варіанти та їхні частоти; складіть варіаційний ряд, для якого знайдіть середнє значення.

Розв’язок

Статистичний ряд даної вибірки: 2, 3, 4, 4, 4, 5, 5, 6, 6, 6.

Варіанти, варіаційний ряд: 2, 3, 4, 5, 6; частоти відповідно дорівнюють 1, 1, 3, 2, 3.

Середнє значення вибірки:
(2 • 1 + 3 • 1 + 4 • 3 + 5 • 2 + 6 • 3) / ( 1+1+3+2+3) = = 45/10 = 4,5

Середнє значення характеризує вибірку в цілому і залежить від усіх її елементів. Воно буде найкращим показником вибірки з великою сукупністю, якщо великі й малі крайні значення трапляються рідко, а середні - часто.

 

Додаток 4

Практичне завдання

Спільне для всіх груп

Об’єднайте дані проведених опитувань з обох класів в одну вибірку. Проведіть статистичні розрахунки для власника взуттєвої крамниці:

1. Запишіть об’єм вибірки n = …

2. Запишіть статистичний ряд вибірки.

3. Дані ряду занесіть у частотну таблицю.

4. Побудуйте полігон частот і гістограму.

5. Знайдіть міри центральних тенденцій:

а) мода Mo =

б) медіана Mе =

в ) середнє значення X =

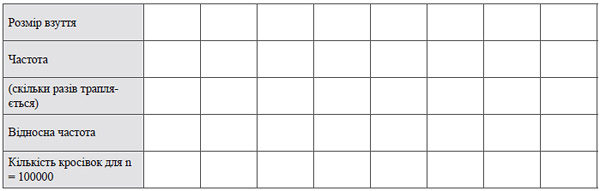
Завдання для аналізу:

Група 1. Запропонуйте рекомендації власникові крамниці щодо кількості кросівок кожного розміру для учнів усієї області. Як ви здійснили обчислення?

Група 2. Взуття якого розміру користуватиметься найбільшим попитом? Яку міру центральних тенденцій ви використали?

Група 3. Чи можна спрогнозувати, яку кількість взуття необхідно закупити, якщо фабрика виготовляє взуття проміжних розмірів (наприклад, 39,5) ? Яким інструментом ви для цього скористувалися?

Група 4. - Наскільки відрізняється середній розмір взуття з однієї групи опитаних учнів від середнього з усієї області? До якого стандартного розміру він наближений? Що це може характеризувати?

Група 5. - Які крайні значення розміру взуття могли б існувати в масштабах області? Обчисліть для власника крамниці кількість взуття цих непопулярних розмірів. Яким інструментом ви скористалися?

 

Додаток 5

Картка самооцінювання учня

Виставте у відсотках (від 0 до 100), наскільки ви почуваєтеся компетентними щодо здобутих на уроці знань та вмінь

 

Додаток 6

Оцінювання роботи малої групи

Ця форма дає можливість оцінити роботу малої групи самими учасниками групи. Можна ставити значок (наприклад, + чи √) у відповідній графі, відзначаючи, як працювала група в цілому, або вписувати імена учасників групи.