Знаходження площі поверхні тіл обертання
Василь Черкач, учитель математики
Рожнівського НВК «Гуцульщина» ім. Ф. Погребенника НАУКМА
Косівського району Івано-Франківської області
Цільова група:
- учні 11 класу
Тривалість:
- 90 хв. (2x45 хв.)
Мета:
- навчити розпізнавати тіла обертання (конус, циліндр, кулю);
- відпрацювати вміння знаходити площу поверхні тіл обертання (конуса, циліндра, кулі);
- розвивати пізнавальний інтерес до предмету, креативне мислення, математичну мову;
- виховати культуру колективної взаємодії, формувати якості, необхідні для ефективної роботи в групі.
Операційні цілі (завдання):
Після закінчення уроку учень знає
- визначення та властивості тіл обертання;
- формули для знаходження площі поверхонь тіл обертання;
розуміє
- спосіб утворення тіл обертання;
вміє
- розрізняти тіла обертання, їхні елементи;
- обчислювати площі поверхонь тіл обертання;
може
- аналізувати проблемну ситуацію;
- визначати перешкоди досягнення результату;
- шукати оптимальні шляхи вирішення проблеми;
- планувати діяльність;
- генерувати пропозиції та робити висновки;
- виявляти ініціативу і вміння вести дискусію.
Методи і техніки:
- метаплан;
- робота в малих группах.
Обладнання:
- маркери;
- аркуші А4;
- ватмани А2 - 4 штуки;
- циркулі, олівці, лінійки;
- клейка стрічка;
- кольоровий папір.
Допоміжні матеріали:
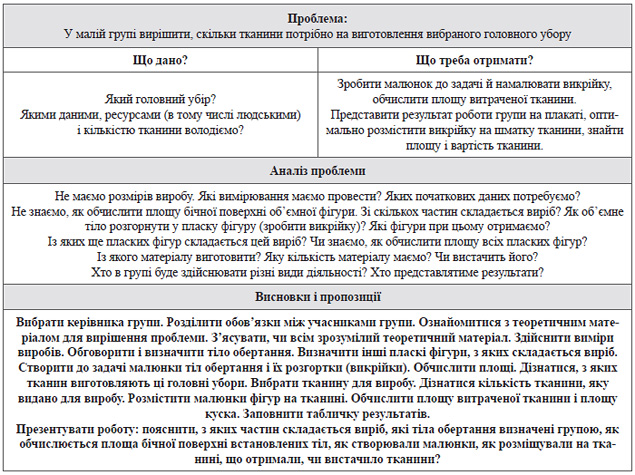
Додаток 2. Схема виконання завдання.
Додаток 3. Рекомендації для вчителя (ведучого дискусії).
Додаток 4. Теоретичний матеріал. Циліндр. Конус. Куля.
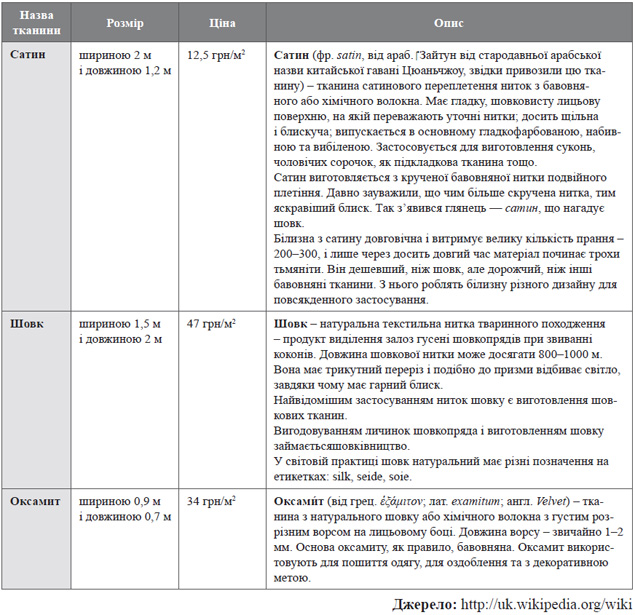
Додаток 5. Відомості про тканину для виготовлення головних уборів.
Додаток 6. Таблиця для презентації розрахунків.
Додаток 7. Критерії оцінювання роботи груп на етапах завдання.
Хід уроку 1
1. Вступна частина
1.1. Повідомте учням тему і мету уроків. Наголосіть, що найважливіше в цій темі - уміння розпізнавати тіла обертання, розуміти спосіб їх утворення та вміти обчислювати площу бічної поверхні. Тіла? оберта?ння - це об’ємні тіла, що виникають при обертанні пласкої фігури, обмеженої кривою, навколо осі, що лежить у тій же площині. Тіла обертання широко використовуються в техніці. Наприклад, в автомобілебудуванні кулі використовують при перемиканні передач, у клапанних пристроях. У формі циліндра виготовлені найважливіші складові частини автомобілів: генератор, конденсатор, фільтр тощо.
1.2. Змоделюйте для учнів ситуацію у вигляді проблемної задачі: Для шкільної вистави необхідно виготовити такі предмети: шапку чарівника, капелюх Кота у чоботях, каску солдатапіхотинця і шапку Знайка (Додаток 1). Для цього треба обчислити мінімальні витрати тканини на виготовлення кожного виробу. Націльте учнів на те, що вони у малих групах цілком самостійно мають розв’язати цю задачу, дійти висновку: які вхідні дані їм необхідні, яких знань не вистачає - і представити результати.
2. Основна частина
2.1. Для реалізації цього завдання і розробки плану дій запропонуйте учням попрацювати, спираючись на наявний у них життєвий досвід.
2.2.Об’єднайте учнів у 4 групи і скажіть, щоб кожна група зайняла місце за окремим столом. Прикріпіть на дошці зразки головних уборів (Додаток 1) без розмірів. Роздайте групам ватман, кольорові картки у формі кола, трикутника, овала і прямокутника, клейку стрічку, маркери.
Коротко поясніть суть вправи та її ціль - проаналізувати ситуацію в загальному вигляді, зосередитися на пошуку способу розв’язання проблеми, виявити прогалини у можливостях досягнення мети, скласти план дій і прийти до спільного рішення, як досягти результату. Запропонуйте записати завдання і вибрати ведучого в кожній групі. Наголосіть, що неправильних думок немає. Націльте ведучих дотримуватися схеми, залучати всіх учасників до процесу. Нагадайте учням про культуру ведення дискусії, попередьте, що вправа триватиме 20 хвилин, і дайте сигнал починати. Пам’ятайте, що ви повинні бути тільки пасивним спостерігачем, - прислухайтеся до обговорення, намагайтеся не поправляти учнів, втручайтеся тільки в разі суперечки або конфлікту.
2.3. Перейдіть до другої частини обговорення. Розмістіть усі плакати з виконаними завданнями на дошці. Дайте можливість усім групам представити власне бачення проблеми. Приступіть до обговорення спільного плану дій на основі плакатів. Якщо потрібно, перекладайте картки, міняйте їх місцями, звертайте увагу учнів на найбільш раціональні висновки. Якщо вважаєте за необхідне, доповніть власними пропозиціями за зразком (Додаток 3).
3. Підсумкова частина
3.1. Підведіть проміжний підсумок першого уроку. Наголосіть, що найважливішим із висновків є усвідомлення потреби нових знань; що для обчислення площі поверхні тіл, утворених шляхом обертання певних геометричних фігур, можна їх розгорнути у пласкі фігури (викрійки) і знайти їхню площу за раніше вивченими формулами. Якщо учні самостійно дійшли такого висновку, то зверніть на це увагу, або ж скажіть, що на наступному уроці вони про це дізнаються.
3.2. Повідомте про свої враження від активності та креативності мислення учнів, уміння давати пропозиції, планувати діяльність і робити висновки.
Хід уроку 2
1. Вступна частина
1.1. Нагадайте учням тему і мету заняття, а також проблемну задачу, до вирішення якої вони вже підійшли зовсім близько.
1.2. Зверніть їхню увагу на схему виконання завдання, подану на дошці, складену на попередньому уроці. Нагадайте, що надалі учні мають дотримуватися напрацьованих пропозицій і послідовності вирішення задачі. Скажіть, що на цьому уроці вони матимуть змогу довести розв’язання задачі до логічного кінця і представити свої напрацювання.
2. Основна частина
2.1. Попросіть учнів повернутися до своїх груп, з якими працювали на попередньому уроці. Роздайте матеріали, яких їм не вистачало для розв’язку задачі (Додатки 1, 4, 5). Запропонуйте самостійно ознайомитися з теоретичним матеріалом (Додаток 4), підкреслити нові терміни. Через 10 хвилин запитайте в учнів, які поняття чи визначення залишилися їм незрозумілі. Поясніть їх. Важливо: запитайте, наскільки прочитане збігається з їхніми висновками про спосіб вирішення задачі.
2.2. Роздайте таблиці для обчислень (Додаток 6), папір, олівці, лінійки, циркулі й маркери. Повідомте учнів, що вони можуть розпочинати вирішувати проблемну задачу, користуючись схемою й отриманими матеріалами. Відведіть на роботу 20 хв.
2.3. Вислухайте презентацію груп щодо виконаної роботи. Заохочуйте інших учнів висловлювати власну думку щодо коректності знайдених результатів. Особливо уважно розберіть помилкові обчислення, попросіть учнів пояснити, як вони мислили. Упевніться, що учні усвідомили помилку.
3. Підсумкова частина
3.1. Підведіть підсумки про спосіб обчислення площі поверхні тіл обертання, наголосіть на важливості теми у повсякденному житті на прикладі вирішеної задачі, дайте усну оцінку самостійній роботі учнів, підкресліть виявлену креативність, творчість, організованість під час роботи в групі. Виставте оцінки згідно з критеріями (Додаток 7).
3.2. На домашнє завдання запропонуйте підготувати презентації «Тіла, утворені обертанням трикутників та чотирикутників».
Головні убори
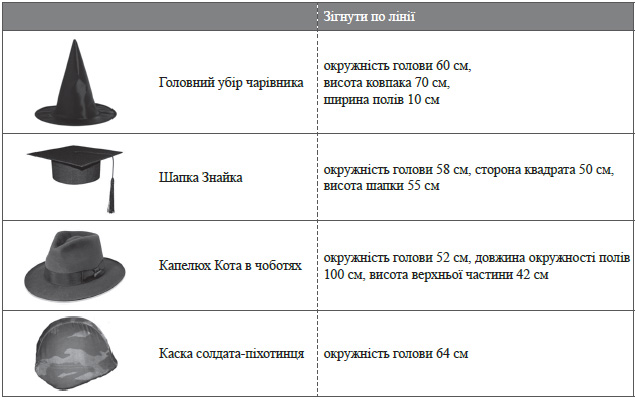
Схема виконання завдання

Рекомендації для вчителя або керівника дискусії (напрямок ведення дискусії)
Теоретичний матеріал
Циліндр
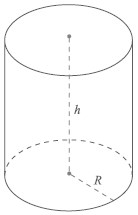
Циліндр (грец. Κύλινδρος - «валик») - геометричне тіло, обмежене замкнутою циліндричною поверхнею і двома паралельними площинами, що перетинають її.
- якщо основи циліндра пласкі - циліндр називають таким, що стоїть на площині;
- якщо основи стоять на площині циліндра і перпендикулярні твірним - прямий циліндр; зокрема якщо основа, що стоїть на площині циліндра:
- коло - круглий циліндр;
- еліпс - еліптичний циліндр.
Елементи циліндра
Круги, що утворюють циліндр, називаються основами циліндра. Вони рівні й лежать у паралельних площинах.
Твірні циліндра - відрізки, що сполучають відповідні точки кіл кругів. Вони паралельні й рівні між собою.
Поверхня циліндра складається з основ і бічної поверхні. Бічна поверхня складається з твірних.
Радіусом циліндра називається радіус його основи. Висотою циліндра називається відстань між площинами основ.
Віссю циліндра називається пряма, яка проходить через центри основ. Вона паралельна твірним.
Осьовий переріз - переріз циліндра площиною, яка проходить через вісь циліндра.
Дотична до циліндра - площина, яка проходить через твірну прямого циліндра і перпендикулярна до осьового перерізу, проведеного через цю твірну, називається площиною. Циліндр називається прямим, якщо його твірні перпендикулярні до площин основ. Прямий циліндр можна розглядати як тіло, утворене обертанням прямокутника навколо його сторони як осі.
Площа поверхні циліндра
Площа бічної поверхні тіл обертання обчислюється за їхньою розгорткою.
Розгортка циліндра – це прямокутник з висотою h і довжиною 2?R, отже, площа
бічної поверхні циліндра дорівнює площі його розгортки та обчислюється за фор-
мулою:
Sh = 2πRh,
Площа повної поверхні циліндра дорівнює сумі площ його бічної поверхні та
його основ:
Sp = 2πR(h + R).
Конус
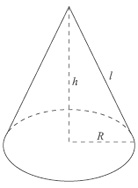 Ко́нус (від грец. Κώνος - «соснова шишка») - геометричне тіло, отримане шляхом об’єднання всіх променів, що виходять з однієї точки - вершини конуса, і таких, що проходять через довільну пласку поверхню. Іноді конусом називають частину такого тіла, отриману об’єднанням усіх відрізків, що з’єднують вершину і точки пласкої поверхні (яку в такому разі називають основою конуса, а конус називають таким, що спирається на дану поверхню). Також можна сказати, що це тіло, отримане при обертанні прямокутного трикутника навколо одного з його катетів.
Ко́нус (від грец. Κώνος - «соснова шишка») - геометричне тіло, отримане шляхом об’єднання всіх променів, що виходять з однієї точки - вершини конуса, і таких, що проходять через довільну пласку поверхню. Іноді конусом називають частину такого тіла, отриману об’єднанням усіх відрізків, що з’єднують вершину і точки пласкої поверхні (яку в такому разі називають основою конуса, а конус називають таким, що спирається на дану поверхню). Також можна сказати, що це тіло, отримане при обертанні прямокутного трикутника навколо одного з його катетів.
Відрізок, опущений перпендикулярно з вершини на площину основи (а також його довжина), називається висотою конуса. Якщо площа основи має скінченне значення, то об’єм конуса також має скінченне значення й дорівнює третині добутку висоти на площу основи. Отже, всі конуси, що спираються на дану основу і мають вершину в площині, паралельній цій основі, мають рівний об’єм, оскільки їх висоти рівні. Якщо основою конуса є многокутник, тоді конус стає пірамідою. Таким чином піраміди є підмножиною конусів.
Відрізок, що сполучає вершину конуса з точкою границі його основи, називається твірною конуса. Множина всіх твірних конуса називається бічною поверхнею конуса.
Площа поверхні конуса
Повна площа прямого кругового конуса
S = πr(r + l),
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Площа бічної поверхні прямого кругового конуса
Sb = πrl,
де r і l – радіус кола основи і довжина твірної бічної поверхні відповідно.
Куля
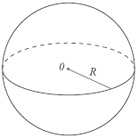 Куля - тіло, утворене обертанням круга навколо його діаметра. Центром кулі називають центр круга, обертанням якого її утворено. Відрізок, який сполучає центр кулі з довільною точкою її поверхні, - радіус кулі. Відрізок, який сполучає дві довільні точки поверхні кулі, - її хорда. Хорда кулі, яка проходить через центр, - діаметр кулі.
Куля - тіло, утворене обертанням круга навколо його діаметра. Центром кулі називають центр круга, обертанням якого її утворено. Відрізок, який сполучає центр кулі з довільною точкою її поверхні, - радіус кулі. Відрізок, який сполучає дві довільні точки поверхні кулі, - її хорда. Хорда кулі, яка проходить через центр, - діаметр кулі.
Куля - це множина всіх точок простору, що перебувають від заданої точки O на відстані, не більшій за дану відстань R. При цьому точка O називається центром, а R - радіусом кулі. Будь-який відрізок, який сполучає центр кулі з точкою кульової поверхні, також називається радіусом.
Поверхня кулі називається сферою. Також дуже часто кулею називають частину простору, обмежену сферою.
Площу сфери, яка обмежує кулю з радіусом R, можна підрахувати за формулою
S = 4πR2.
Площа поверхні кулі є найменшою серед площ поверхонь стереометричних тіл з однаковим об’ємом.
Відомості про тканину для виготовлення головних уборів
Таблиця для презентації розрахунків

Критерії оцінювання роботи груп на етапах завдання
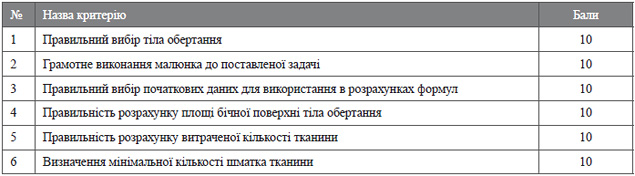
46-60 балів - «високий рівень»
30-45 балів - «достатній рівень»
16-30 балів - «середній рівень»
1-15 балів - «початковий рівень»
Инвестор Аркадий Морейнис в Telegram-канале «Тёмная сторона» рассказал, как доступно объяснить ребенку суть предпринимательства.
7-8 грудня в Університеті банківської справи пройдуть півфінальні та фінальні ігри ІV Всеукраїнського турніру юних знавців курсу «Фінансова грамотність».